Circumventing the Solution of Inverse Problems in Mechanics through Deep Learning: Application to Elasticity Imaging

Abstract

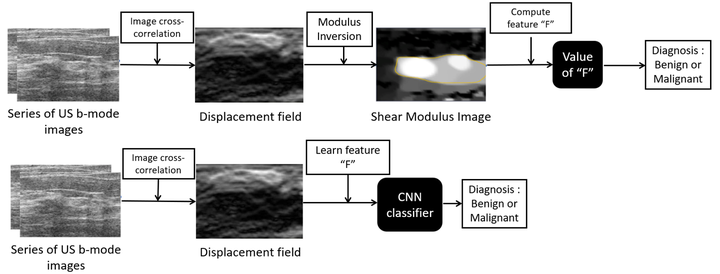
The ability to make decisions based on quantities of interest that depend on variables inferred from measurement finds application in different fields of mechanics and physics. The evaluation of the inferred variables, and hence the quantities of interest, from the measurement typically requires the solution of an inverse problem. For example, in medical imaging the elastic heterogeneity of a tumor and its nonlinear elastic response can be used to distinguish benign tumors from their malignant counterparts. These images of linear and nonlinear elastic parameters of tissue are typically obtained by using a measured displacement field and solving a complex inverse elasticity problem. In this paper we consider circumventing the solution of the inverse problem by using measured displacements as input to a deep convolutional neural network (CNN) and training it to classify tumors on the basis of their elastic heterogeneity and nonlinearity. For a simple, 5-layer CNN trained with 8,000 samples for heterogeneity, and a 4-layer CNN trained with 4,000 samples for nonlinear elasticity we report classification accuracies in the range of 99.7% - 99.9%. The training and testing data are both obtained from the forward solution of finite element models of samples. We also analyze the weights of the trained model to understand the process through which the network extracts features of elastic moduli from the input displacement images. Finally, we apply the nonlinear elasticity classifier, which is trained entirely using simulated data, to displacement images obtained from ten patients with breast lesions and note that it correctly classifies eight out of ten cases. This application illustrates how data from physics-based models can be used in improving the performance of a data-driven algorithm in data-sparse scenarios.